An Invitation to Higher Gauge Theory (Again)

This paper may be finished now:

John Baez and John Huerta, An Invitation to Higher Gauge Theory.

Tim van Beek wanted a heads-up when it was done, so he could make another round of corrections. Indeed, I’d love comments from all of you!

There are lots of juicy example applications in this paper! The idea is to get lots of theoretical and mathematical physicists to see those examples without requiring them to already be experts on category theory. They will then fall in love with $n$ -categories, turn into an army of Urs Schreiber clones, and take over the universe. My duty to mathematical physics thus fulfilled, I can focus my energies on saving the planet.

That’s the plan, anyway. Sounds like a comic book. Here’s how the paper goes:

In Section 1 we start by explaining categories, functors, and how parallel transport for particles can be seen as a functor taking any path in a manifold to the operation of parallel transport along that path. In < a href http://math.ucr.edu/home/baez/invitation_2.pdf#page=11″>Section 2 we ‘add one’ and explain how parallel transport for particles and strings can be seen as ‘2-functor’ between ‘2-categories’. This requires that we generalize Lie groups to ‘Lie 2-groups’. In Section 3 we describe many examples of Lie 2-groups, and sketch some of their applications:

shifted abelian groups, $U(1)$ gerbes, and their role in string theory and multisymplectic geometry
the Poincaré 2-group and the spin foam model for 4d Minkowski spacetime
tangent 2-groups, 4d $B F$ theory and topological gravity
inner automorphism 2-groups and 4d $B F$ theory with cosmological constant term
automorphism 2-groups, nonabelian gerbes, and the gravity 3-group
string 2-groups, string structures, the passage from Lie $n$ -algebras to Lie $n$ -groups, and the Lie 3-superalgebra governing 11-dimensional supergravity

Finally, in Section 4 we discuss gauge transformations, curvature and nontrivial 2-bundles.

This entry was posted on March 18, 2010 at 1:49 pm and is filed under Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. Responses are currently closed, but you can trackback from your own site.

9 Responses to “An Invitation to Higher Gauge Theory (Again)”

Tim van Beek Says:
March 18, 2010 at 2:33 pm
John wrote:

Tim van Beek wanted a heads-up when it was done…

Thanks! This way I don’t have to perform busy waiting.

…so he could make another round of corrections.

Actually I read it because I find it interesting, and because I’m allowed to ask questions about it here, that one or two of those may help you to improve the paper is a tradeoff.

(Please cut me some slack if it takes me a couple of days to report back, time management is a challenge right now).

My duty to mathematical physics thus fulfilled…

Don’t know if it goes without saying: I hope you are going to visit math phys often for the fun of it…
John Baez Says:
March 18, 2010 at 4:39 pm
Thanks for your interest in the paper, Tim. I’m sorry for suggesting that you’d volunteered to be an unpaid copy-editor producing lists of typos at a moment’s notice!

John Huerta spotted a mistake in the calculation of how the curvature 2-form transforms under gauge transformations, which I need to fix now.

Urs Schreiber suggested some major improvements in my discussion of the “gravity 3-group”, and I need to make those now.

Chris Schommer-Pries and David Roberts also suggested improvements.

Don’t know if it goes without saying: I hope you are going to visit math phys often for the fun of it…

I will. Actually, I plan to help everyone see that applications of math to geology, meteorology, population biology, engineering, computer science and the like are just as interesting as applications to particle physics and quantum gravity. In fact more so, because you can do something good for your planet while having fun with abstract concepts. By the end of the century our image of mathematical physics may be very different than now.

I’m dipping my toe in the water at the end of May, when I’ll give a talk on electrical circuits at Dennis Sullivan’s seminar. It will contain a few surprises, I hope.
Tim van Beek Says:
March 18, 2010 at 8:31 pm
John wrote

I’m sorry for suggesting that you’d volunteered to be an unpaid copy-editor producing lists of typos at a moment’s notice!

No need to apologize, I wasn’t complaining: I have to review documents in my everyday job regularly, and usually the deadline for feedback is a week, at most, so I just wrote what I write most people who ask me for a review (“got your note, will look into it, will take a couple of days”).
johncarlosbaez Says:
March 19, 2010 at 12:24 am
Okay, Tim. Don’t bother downloading the paper until you actually want to read it, because it’s getting better with time. For example, by now I’ve dealt with all the aforementioned problems.
ursschreiber Says:
March 19, 2010 at 7:52 am
On p. 31 you have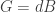 $G = d B$ . The notation most people will be familiar with for the field strength of the Kalb-Ramond field and will recognize in other articles is 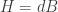$H = d B$ . Wouldn’t that be better?
Mihai Cartoaje Says:
March 19, 2010 at 9:48 pm
The curvature of a Cartan connection A is,
$\mathrm{d} A + \frac{1}{2}[A, A]$
with,
$[A, B] (X, Y) = [A (X), B(Y)] - [A (Y), B(X)]$
with the commutator evaluated in a Lie algebra.

For example, if a group is,
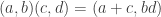
$(a, b)(c, d) = (a + c, bd)$
its Lie algebra is,
$[(\epsilon, 1), (0, 1 + \epsilon)] = (\epsilon, 1 + \epsilon) - (\epsilon + \epsilon^2, 1 + \epsilon) =$
$= (-\epsilon^2, 0)$
$[X, Y] = -X$

The Maurer-Cartan form is,
$A^0 = \frac{1}{y} \mathrm{d}x$
$A^1 = \frac{1}{y} \mathrm{d}y$
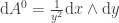
$\mathrm{d} A^0 = \frac{1}{y^2} \mathrm{d}x \wedge \mathrm{d}y$
$\mathrm{d} A^1 = 0$

The horizontal component of the curvature is,
$\mathrm{d}A^0 (X, Y) + [A (X) , A (Y)] = \frac{1}{y^2} + [\frac{1}{y} X, \frac{1}{y} Y]$
$= \frac{1}{y^2} + \frac{1}{y^2} [X, Y]$
$=\frac{1}{y^2} - \frac{1}{y^2}$
$= 0$

The vertical component of the curvature is,
$\mathrm{d}A^1(X, Y) + [A (X) , A (Y)] = 0 + \frac{1}{y^2} [X, Y]$
$= 0$

So the curvature is,
$\mathrm{d} A + \frac{1}{2}[A, A] = 0$
- Mihai Cartoaje Says:
  March 19, 2010 at 10:22 pm
  For the definition of the example group, I should have written,
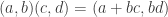
  $(a, b) (c, d) = (a + bc, bd)$
Tim van Beek Says:
March 20, 2010 at 10:32 am
Finally made my way through the version I got yesterday afternoon (CET), and it looks pretty much completed.

Repeating myself: It is a joy to read! Here are some aspects of what I like most:

* simple yet helpful pictures,

* motivational handwaving, clearly pointed out as such, plus the information if it can be made precise plus references,

* simple analogies that pick up the reader where she/he stands, to new concepts that are stated in a way where the analogy is even mirrored in the very phrasing…(list could go on).

In fact, I have only two suggestions for additional references:
If you like to, you could mention the Aharonov–Bohm effect on page 28 or 34. Likewise, you could mention the term “anyon” on page 34 where you mention particles with “exotic statistics” (once people know the keyword, they can look it up in wikipedia, which already has a nice article with references).

I’m completly unperturbed by typos as long as I still get the meaning (you may have noticed that I cannot write one single post without one), but some readers will infer from the existence of typos that the authors are generally sloppy – I mean, more serious readers than those who managed to raise item 20 on the crackpot index (“if he can’t spell Einstien, what are the chances he understands relativity?”).

So here we go:

* Abstract: “which has topological topological gravity”

* p3: “You should think of of objects”

* p6 bottom: “We define [the] path groupoid”

* p12: the horizontally composition picture: right side should go from x to z, but goes to y instead.

* p13: interchange law, equation, right side: both indexes are 1 in the first bracket, the first one should be 2.

* p13: “the path groupoid of a spacetime manifold describes all the possible motions of a point particle”: Maybe “phase space” would be better than “spacetime”, because you did not exclude spacelike paths 🙂

* p14: “The key idea [is] to define a concept of ‘thin homotopy’…”

* p30: “This also [has] a higher version, which dates back to 1935…”

* p38: “…the previous section is close[ly] related…”

* p38: “…conditions of Theorem [broken link]”

* p.39: “it suffices suffices”, and alpha is missing some tex tags twice

* p40: “…a vector space equipped with [a] nongenenerate…”

* p43: “Then [a] gauge transformation…”

* p46: “…the holonomy over a surface will not changee if [we] apply a smooth homotopy…”

* p47: “…if the the transition functions satisfy a…” and “readibility” instead of “readability”

* p52: “Conversely, any closed, integral 2-form F on M [is] the curvature of come…”

P.S.: If you feel the need to balance your karma, may I ask you to proofread some pages on the nLab about axiomatic and constructive QFT in a few months? (Even superheroes need some distraction from time to time, from the consuming task of saving the planet 🙂
John Baez Says:
March 23, 2010 at 4:28 am
Thanks very much, Tim, for your comments!

If anyone has further comments, please post them here at the old Café, which seems to be working again.